Sumatoare
Sumatorul elementar
Sumatoarele (adders), folosite cel mai mult în unitățile aritmetice logice ale procesoarelor, realizează adunări pe un număr dat de biți, furnizând la ieșirea circuitului suma și transportul (carry) rezultat în urma operației.
Există mai multe tipuri de sumatoare pentru adunarea numerelor pe n biți, iar acestea se bazează pe sumatoare simple de 1 bit, care pot fi de două tipuri:
- sumatorul elementar parțial (Half adder) - însumează doi operanzi pe 1 bit și oferă la ieșire suma acestora și transportul.
- sumatorul elementar complet (Full adder) - însumează doi operanzi pe 1 bit și un transport și oferă la ieșire suma acestora și transportul.
Figure: Diagrama bloc pentru half adder
Figure: Diagrama bloc pentru full adder
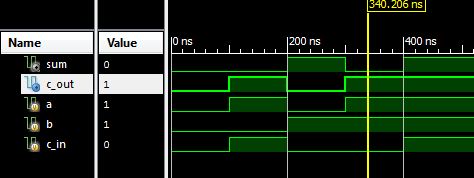
Figure: Diagrama semnale pentru full adder
Sumatorul elementar parțial
Acest sumator este în continuare descris prin expresiile booleene, tabelul de adevăr și schema logică.
| a | b | sum | c_out |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Table: Tabelul de adevăr pentru sumatorul elementar parțial
Din tabelul de adevăr se pot deduce următoarele formule:
sum = a ^ b
c_out = a && b
Conform acestor formule putem exprima circuitul prin porți logice, ca în imaginea de mai jos:
Figure: Schema logică pentru half adder
Dintr-un tabel de adevăr, pentru fiecare output se va deduce o funcție/expresie aplicând următoarele reguli:
- fiecare rând din tabel pentru care funcția are valoarea 1 va genera un termen
- termenii sunt formați din parametrii funcției legați prin ȘI
- dacă parametrul are valoarea 1 se consideră în formă directă
- dacă parametrul are valoarea 0 se consideră în formă negată
- se aplică SAU între toți termenii deduși
Pentru sumatorului elementar parțial avem:
void half_adder(const int a, const int b, int &sum, int &carry) {
sum = a ^ b; // Sum is the XOR of the inputs
carry = a & b; // Carry is the AND of the inputs
}
Codul sursa pentru functia half_adder
În multe cazuri aceste formule sunt prea complexe, conținând multe operații și necesitând multe porți logice pentru a fi implementate. Pentru a reduce complexitatea formulelor rezultate se poate aplica un procedeu de minimizare, care va reduce dimensiunea termenilor sau chiar îi va elimina. Minimizarea se poate realiza folosind teoremele algebrei booleene sau grafic, prin diagrame Karnaugh.
Sumatorul elementar complet
| a | b | c_in | sum | c_out |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Table: Tabelul de adevăr pentru full adder
Din tabelul de adevăr se pot deduce următoarele formule:
sum = a ^ b ^ c_in
c_out = ((a ^ b) && c_in) || (a && b)
Conform acestor formule putem exprima circuitul prin porți logice sau putem folosi sumatoare elementare parțiale, ca în imaginea de mai jos:
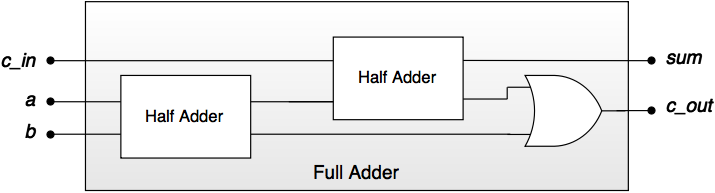
Figure: Schema logică pentru full adder
void full_adder(const int a, const int b, const int cin, int &sum, int &carry)
{
sum = a ^ b ^ c_in;
carry = ((a ^ b) && c_in) || (a && b);
}
Sau utilizand sumatoare elementare partiale:
void full_adder(const int a, const int b, const int cin, int &sum, int &carry) {
int sum1, carry1, carry2;
// First half adder
half_adder(a, b, sum1, carry1);
// Second half adder
half_adder(sum1, cin, sum, carry2);
// Final carry
carry = carry1 | carry2;
}
Codul sursa pentru functia full_adder
Sumatorul cu transport succesiv
Cel mai intuitiv mod de a forma un sumator este de a lega în cascadă mai multe sumatoare elementare complete pe 1 bit. În acest fel se formează un sumator cu transport succesiv (eng. ripple-carry adder), cum este cel pe 4 biți din imaginea de mai jos, care primește la intrare a[3:0], b[3:0], c_in și are ca ieșiri suma s[3:0] și transportul c_out. În cazul sumatoarelor pe mai mulți biți nu mai este indicat de pornit întâi de la o tabelă de adevăr deoarece aceasta ajunge la dimensiuni prea mari.
Figure: Schema sumatorului cu transport succesiv, pe 4 biți
template <int N>
void ripple_adder(const int (&a)[N], const int (&b)[N], int (&sum)[N], const int carry_in, int &carry_out) {
// Initialize carry to 0
int carry_tmp[N+1];
carry_tmp[0] = carry_in;
// Iterate over each bit
for (int i = 0; i < N; ++i) {
// Calculate the sum and carry for the current bit
full_adder(a[i], b[i], carry_tmp[i], sum[i], carry_tmp[i+1]);
}
// Set the final carry
carry_out = carry_tmp[N];
}
Codul sursa pentru functia ripple_adder
Un alt avantaj al acestui design simplu, este că se pot forma sumatoare pe mai mulți biți din înlănțuirea oricâtor sumatoare. De exemplu, pentru a însuma numere pe 16 biți se poate crea un sumator ripple-carry din legarea în cascadă a 4 sumatoare pe 4 biți, ca în imaginea de mai jos.
Figure: Schema sumatorului cu transport succesiv, pe 16 biți
// Example for 16-bit ripple adder using four 4-bit ripple adders
const int M = 16;
int a16[M] = {1, 0, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 0}; // Example 16-bit binary number
int b16[M] = {1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1}; // Example 16-bit binary number
int sum16[M];
int carry16[5] = {0}; // Carry array for each 4-bit adder
for (int i = 0; i < M; i += 4) {
ripple_adder<4>(*(int(*)[4])(a16 + i), *(int(*)[4])(b16 + i), *(int(*)[4])(sum16 + i), carry16[i / 4], carry16[i / 4 + 1]);
}