Lab 1 - Number Representation

Task: Conversions

Perform the following conversions between numbering systems:

a. From decimal to binary and hexadecimal:

• 121
• 18446

b. Convert to decimal:

• 0b1100010111010010
• 0xBB29

c. From hexadecimal to binary:

• 0x5E
• 0x4A01

d. From binary to hexadecimal:

• 0b01111101
• 0b1000110000011111

If you're having difficulties solving this exercise, go through this reading material.

Task: Rotations

You will solve the exercise starting from the file rotations.c located in the directory drills/tasks/rotations/.

Implement left and right rotations for 32-bit integers in C.

TIP: The rotation operation (also known as circular shift) is similar to the shift operation, with the only difference being that the empty space generated by the shift is filled with the discarded bit.

Example of left rotation by one bit:

NOTE:

rotate_left(0x80000000, 1)   = 1
rotate_right(0x00000001, 16) = 65536

If you're having difficulties solving this exercise, go through this reading material.

Task: Binary Even and Hexadecimal Odd

You will solve the exercise starting from the file odd_even.c located in the directory drills/tasks/odd-even/.

Traverse an array of 32-bit integers using pointer operations and display the even numbers in binary and the odd numbers in hexadecimal.

NOTE: Use bitwise operations wherever possible in your solution!

NOTE: For the array [214, 71, 84, 134, 86], the program will display:

0b11010110
0x00000047
0b01010100
0b10000110
0b01010110

If you're having difficulties solving this exercise, go through this reading material.

Task: Length and Equality with Bitwise Operations

You will solve the exercise starting from the file len_xor.c located in the directory drills/tasks/len-xor/support/.

For a given string of characters, display:

• the length of the string
• the address of each character at position i that is equal to the character at position $i + 2^i$ (if $i + 2^i$ exceeds the size of the string, use the modulo operation)

Use pointer operations and bitwise operations as much as possible!

NOTE: Do not use functions such as strlen(), sizeof(), pow(), and do not check equality using ==. Also, do not access string elements in the form of s[i].

TIP: For the string "aac":

length = 3
Address of a: 0x564c364482a0
Address of a: 0x564c364482a1

For the string "ababababacccbacbacbacbacbabc":

length = 28
Address of b: 0x563f0da6f2a1
Address of a: 0x563f0da6f2a2
Address of c: 0x563f0da6f2a9
Address of a: 0x563f0da6f2b0
Address of b: 0x563f0da6f2b2
Address of b: 0x563f0da6f2b5
Address of c: 0x563f0da6f2b7
Address of a: 0x563f0da6f2b9

The above addresses are illustrative!

If you're having difficulties solving this exercise, go through this reading material.

Task: Reversing a String

You will solve the exercise starting from the file mirror.c located in the directory drills/tasks/mirror/support/.

Using pointer operations, implement a C program that reverses a string of characters. The mirror function should perform an in-place reversal of the characters in the string (upon exiting the function, the input string will contain the reversed string).

NOTE: Do not access string elements using the form s[i].

TIP:

mirror("AnaAreMere") = "ereMerAanA"

mirror("asdfghjl") = "ljhgfdsa"

mirror("qwerty") = "ytrewq"

If you're having difficulties solving this exercise, go through this reading material.

Binary and Hexadecimal Systems

For representing information (instructions and data), computers use the binary system (base 2). When writing programs in assembly language, the hexadecimal system (base 16) is preferred because it saves the programmer from writing long strings of 1s and 0s, and conversion to/from binary can be done much more easily than with the decimal system (base 10).

NOTE: We'll use the prefix 0b for representing numbers in binary and 0x for hexadecimal numbers. For example, we can write the unsigned integer 127 as 0b01111111 or 0x7F.

Binary System

In the binary system (base 2), values are represented as a string of 0s and 1s. Each digit in the string represents a bit, and a group of 8 bits forms a byte. A group of 4 bits is called a nibble or half-byte.

Operations with Values Represented in Binary

Arithmetic Operations

Arithmetic operations are the classic +, -, *, / (integer division), % (modulo). Fundamentally they work the same way in any base 10, 2, 16 etc. Just keep in mind what the maximum digit is for each of these bases so you know when to carry or subtract 1 to or from the higher-order digit of the result or operand.

You can find a few examples of arithmetic operations in base 2 here

Logical Operations

Operators on Binary Values

• NOT Operation: Inverts each bit.

Example:

INV(0b10011010) = 0b01100101

• Logical AND Operation: Performs the 'and' operation between bits at the same positions in operands.

Example:

0b1001 AND 0b0111 = 0b0001

• Logical OR Operation: Performs the 'or' operation between bits at the same positions in operands.

Example:

0b1001 OR 0b0111 = 0b1111

• Exclusive OR (XOR) Operation:

If bits at the same positions in operands have equal values, the resulting bit is 0; otherwise, it's 1.

Example:

0b1001 XOR 0b0111 = 0b1110

Logical Shifts

Logical shifts left/right involve moving each bit by one position. Since the result must be on the same number of bits as the initial value, the first bit is lost, and the empty space is filled with a 0 bit.

For explanations related to bitwise operations in C, refer to the guide at Bitwise Operators in C.

Hexadecimal System

In the hexadecimal system (base 16), values are represented as a string of characters from '0' to '9' or 'a' to 'f'. A byte consists of two such characters, so each character corresponds to a group of 4 bits (a nibble).

Conversion from Decimal to Binary/Hexadecimal

• Divide the number successively by the base number (2 or 16) and keep the remainders.
• When the quotient of the division becomes 0, write down the remainders in reverse order.
• In the case of base 16, when the remainder is greater than 9, letters a-f are used (0xa = 10, 0xf = 15).

Example: Conversion of the number 0xD9B1 to decimal

$$\texttt{0xD9B1} = 1 \cdot 16 ^ 0 + 11 \cdot 16 ^ 1 + 9 \cdot 16 ^ 2 + 13 \cdot 16 ^ 3 = 55729$$

Conversion between Binary and Hexadecimal

As mentioned earlier, a digit in a hexadecimal number corresponds to a group of 4 bits (a nibble). Therefore, to convert a number from hexadecimal to binary, it's sufficient to transform each digit into the equivalent 4-bit group.

Example: Conversion of the number 0xD9B1 to binary

• 0x1 = 0b0001
• 0xB = 0b1011
• 0x9 = 0b1001
• 0xD = 0b1101

Thus, the resulting binary number is 0b1101100110110001.

The reverse operation, conversion from binary to hexadecimal, can be done by converting each group of 4 bits into the corresponding digit in hexadecimal.

Use of Base 16 Representation

The hexadecimal system is used to represent memory addresses and to visualize data in a more interpretable way than a sequence composed only of 0s and 1s. The image below provides an example in this regard:

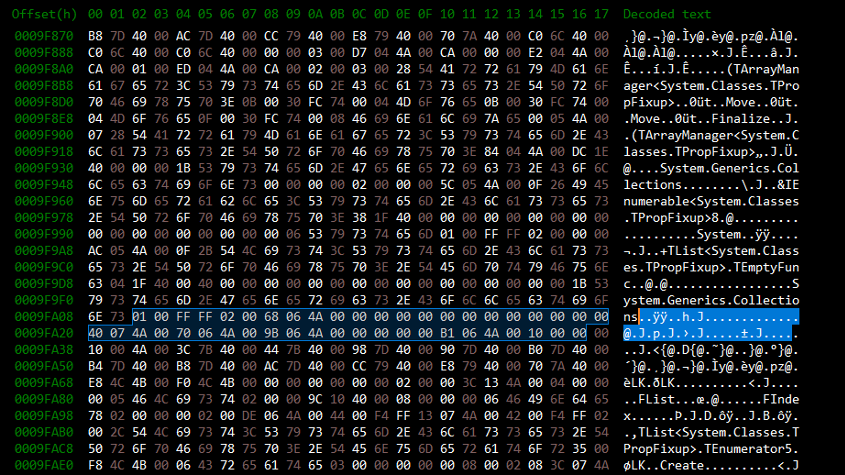
(Image taken from Digital Detective)

Representation of Data Types

In a computer's memory, a value is stored on a fixed number of bits. Depending on the architecture, each processor can access a maximum number of bits in a single operation, which represents the word size.

The sizes of common data types used in C are dependent on both the processor and the platform on which the program was compiled (operating system, compiler). The table below presents the sizes of data types on a 32-bit architecture processor, when the program is compiled using gcc under Linux.

On the left side of the image above, we have memory addresses where data is located. At address 0x0009FA08, the first 4 bytes starting from offset 0x02 are 0x01 0x00, 0xFF, 0xFF. These can represent a 4-byte integer, 4 characters, or 2 integers on 2 bytes. By using base 16, we can interpret the data and infer what they might represent.

The table below shows the sizes of data types on a 32-bit processor.

Data Type	Number of Bits	Number of Bytes
char	8	1
short	16	2
int	32	4
size_t	32	4
long	32	4
long long	64	8
pointer	32	4

On a 64-bit machine, the table above still holds true except for the types below. On 64-bit processors, addresses are 64 bits wide, which obviously affects the size of pointers and size_t.

Data Type	Number of Bits	Number of Bytes
size_t	64	8
long	64	8
pointer	64	8

Order of Representation for Numbers Larger than One Byte (Little-Endian vs Big-Endian)

For representing values larger than one byte, there are two possible methods, both used in practice:

• Little-Endian: The least significant byte is stored first (bytes are stored in reverse order). This model is used by the Intel x86 processor family.

• Big-Endian: The most significant byte is stored first.

Example: We want to store the value 0x4a912480 in memory on 32 bits (4 bytes), starting at address 0x100, using both methods:

Method	Address 0x100	Address 0x101	Address 0x102	Address 0x103
Little-Endian	0x80	0x24	0x91	0x4a
Big-Endian	0x4a	0x91	0x24	0x80

Pointers in C

In the C language, a pointer is a variable whose value is the address of another variable. We can think of a pointer as an intermediary, namely a variable that points to a final location or to another intermediary as shown in the image and code below.

##include <stdio.h>

int main()
{
    int v;
    int *p;  /* pointer to a 32-bit integer */
    int **pp;  /* pointer to a pointer holding the address of a 32-bit integer */

    /* To access the address of a variable in C, we use the address-of operator '&' */
    p = &v;  /* p holds the address of value v */
    pp = &p;  /* pp holds the address of the address of value v */

    v = 69;
    /* To access the value at the address stored by a pointer, we use the dereference operator '*' */
    printf("v(%d) - *p(%d) - **pp(%d)\n", v, *p, *(*pp));  /* outputs v(69) - *p(69) - **pp(69) */

    return 0;
}

Advantages of Pointers

• Pointers are used in creating complex data structures such as linked lists, trees, graphs, hash tables, etc.
• Pointers are used to transfer information between different functions or recursive calls without using global variables.
• By using pointers, we can dynamically allocate memory.
• We can have other functions, strings, complex data structures as parameters for functions.

Disadvantages of Pointers

• Using an uninitialized pointer in a program leads to a segmentation fault by accessing a restricted memory area.
• Manual memory deallocation is required by the programmer for dynamically allocated memory.
• Dereferencing is needed to access a value, which is slower than direct access.

In C, a pointer can be defined for any of the data types existing in the language as well as for void. A void pointer differs from a pointer to an explicit data type in that a void pointer CANNOT be used in pointer operations, as void does not have a clear size. A basic example where pointers and pointer operations are used is the allocation and traversal of an array of values:

##include <stdio.h>
##include <stdlib.h>

##define ARR_LENGTH 5

int main()
{
   int *arr, i;

   arr = (int *)malloc(sizeof(int) * ARR_LENGTH);
   // arr = (int *)calloc(ARR_LENGTH, sizeof(int));

   for (i = 0; i < ARR_LENGTH; ++i) {
       /*
        * arr + i iterates through the addresses of each element in the array, but the address arr + i doesn't increase by i but by i * sizeof(int), as arr is a pointer to int
        * This operation is not visible or necessary in C but will be required later in assembly language
        */
       printf("arr[%d] = %d: ", i, *(arr + i));
   }

   free(arr);
   return 0;
}

Pointers offer great flexibility regarding memory access. Below is an example that checks if a system is little or big endian using casting between different types of pointers.

##include <stdio.h>

int main()
{
    int v = 0x00000001;
    unsigned char *first_byte = (unsigned char *)&v;

    if (*first_byte == 0x01)
        printf("little-endian\n");
    else
        printf("big-endian\n");

    return 0;
}